Treaps: A Hybrid Data Structure
How to Combine Trees and Heaps for Efficient Data Management.
Hi Friends,
Welcome to the 156th issue of the Polymathic Engineer newsletter.
This week, we will take a closer look at treaps, a hybrid data structure that beautifully combines the best properties of binary search trees and heaps.
If you have worked with binary search trees, you know they are great for maintaining sorted data and providing fast lookups. If you have used heaps, you know how well they track the highest- (or lowest) priority element. But what if you need both features in a single structure?
That’s precisely where treaps shine. The name itself comes from the words "tree" and "heap," and that's what they are: a hybrid data structure that keeps elements in sorted order while simultaneously tracking priorities.
The outline will be as follows:
Multi-Dimensional Data Indexing
Combining Trees and Heaps
How Treaps Work
The Balance Problem and Randomization
Applications and Use Cases
Multi-Dimensional Data Indexing
Imagine you are building a task management system for a development team. Each task has a unique identifier (e.g., “bug-1247” or “feature-dark-mode”) and a priority score. The priority score is based on how important the task is to the business, how quickly it needs to be done, and how many other tasks it depends on.
Your system needs to support two critical operations:
Search for a specific task by its identifier to update details like status, assignee, or description.
Retrieve the highest-priority task that should be worked on next.
Both operations need to be fast, because developers use the system all day long.
The straightforward approach is to use a hash table for the tasks. Hash tables provide O(1) average-case lookups by identifier, which handles the first requirement perfectly. However, it becomes difficult to find the highest-priority job. You would need to scan through all the n tasks to find the one with the maximum priority, and that results in O(n) time complexity.
Another option is to use a min-heap ordered by priority. You can always get to the top priority task in a heap in O(1) time, but it takes O(log n) time to extract it. The trouble now moves to the search process. Heaps aren’t meant for quick, key-based searches. To find a specific task by its identifier, you have to scan the whole heap, which takes O(n) time.
At this point, you might consider using both structures simultaneously: a hash table for fast lookups and a heap for priority tracking. This approach works but comes with several challenges. First, you need twice the memory since each task is stored in both structures. Second, you need to keep both structures synchronized. When you update a task’s priority, you must update it in both places. When you delete a task, you must remove it from both structures.
The main problem is that each task has two dimensions: its identifier and its priority. We need a data structure that can efficiently manage operations on both dimensions without the overhead of maintaining two separate structures.
This is where treaps come in. They natively support fast key-based search and provide quick access to the element with the highest priority. In the following sections, we’ll see how treaps achieve this by combining the structural properties of trees and heaps in a single data structure.
Combining Trees and Heaps
Treaps solve the problem of multidimensional sorting by making sure that the same data structure satisfies two distinct constraints for ordering.
The first constraint comes from binary search trees. Every node in a BST is associated with a key. The keys in its left subtree are smaller, and the keys in its right subtree are larger. This property enables efficient search operations, as you can traverse the tree by comparing keys and selecting the appropriate branch at each node.
The second constraint comes from heaps. In a min-heap, the priority of any node is no greater than the priorities of its children. This property makes sure that the node with the lowest priority value is always at the root of the tree.
The key concept is that you can apply these two constraints to different attributes of the same data. In our task management example, the task identifiers follow the BST (horizontal) ordering constraint, while the priority scores follow the heap (vertical) ordering constraint.
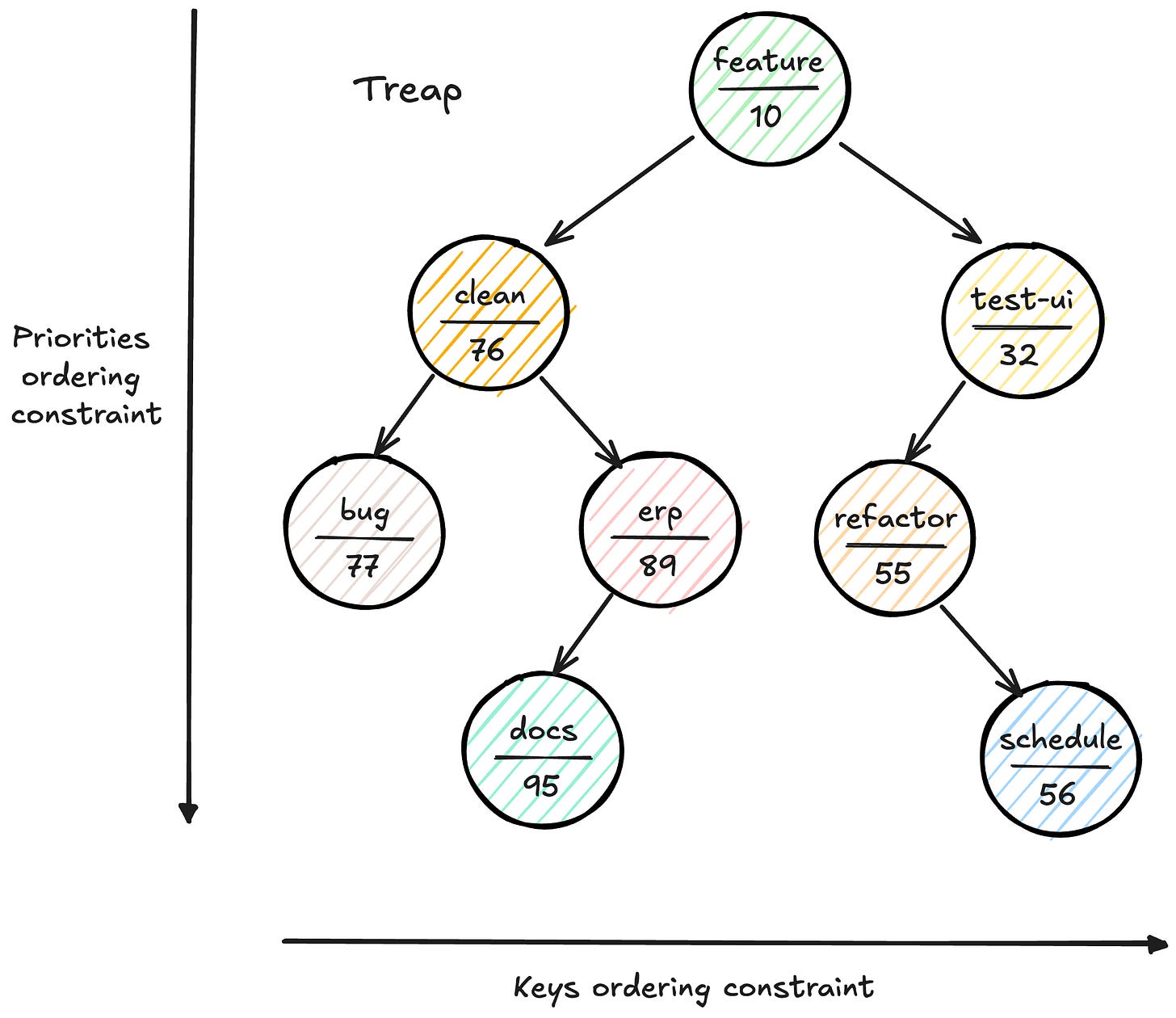
Let’s look at a concrete example to better understand. If we have seven tasks with the following identifiers and priorities: (“bug-1247”, 77), (“feature-auth”, 10), (“refactor-db”, 55), (“docs-api”, 95), (“test-ui”, 32), (“clean backlog”, 76), (“erp”, 89), (“schedule call”, 56).
In a treap, these tasks might be organized as follows:
The root contains “feature-auth” (priority 10) because it has the highest priority
“bug-1247”, “docs-api”, “clean backlog”, and “erp“ are in the left subtree because they come before “feature-auth” alphabetically
“refactor-db”, “test-ui”, and “schedule call” are in the right subtree because they come after “feature-auth.”
Within each subtree, the heap property is maintained for priorities
This structure allows you to search for “clean-up repo” by traversing left from the root (following the BST property). At the same time, the root is always where you may find the highest-priority task (following the heap property).
The hard part is making sure that both constraints are met when adding or removing nodes. You can’t just use standard BST operations because they might not follow the heap property. In the same way, you can’t use standard heap operations because they might not follow the BST property.
The solution is to use a special operation called rotation, which allows you to change the tree structure so the heap property is restored without violating the BST ordering.
How Treaps Work
Now that we understand what treaps are, let’s see how they actually work. We’ll start with the data structure representation, then explore rotations, and finally look at the main operations.
Node Structure
A treap node needs to store more information than a regular BST node. Here is a basic implementation:
class Node:
def __init__(self, key, priority):
self.key = key
self.priority = priority
self.left = None
self.right = None
self.parent = None
def is_leaf(self):
return self.left is None and self.right is None
def is_root(self):
return self.parent is None
def is_left_child(self):
return self.parent is not None and self.parent.left == self
def is_right_child(self):
return self.parent is not None and self.parent.right == self
class Treap:
def __init__(self):
self.root = None
def _set_left(self, parent, child):
"""Helper to set left child and update parent reference."""
parent.left = child
if child is not None:
child.parent = parent
def _set_right(self, parent, child):
"""Helper to set right child and update parent reference."""
parent.right = child
if child is not None:
child.parent = parent
Each node stores its key, priority, and references to its left, right, and parent children. The parent reference is not strictly necessary, but it makes rotations much easier to implement.