Mastering the Two-Pointers Technique

How to use the two-pointer method to efficiently solving array and string problems (with code templates).

Hi Friends,

Welcome to the 124th issue of the Polymathic Engineer newsletter.

This week, we’ll have an overview on Chaos Engineering, an approach to testing that uses intentional failure to make distributed systems more resilient.

The outline will be as follows:

• What is the two pointers method?

• Core strategies and templates

• Classic two-pointer problems

• The next permutation problem

• Practical Implementation Tips

---

Project-based learning is the best way to develop technical skills. CodeCrafters is an excellent platform for practicing exciting projects, such as building your version of Redis, Kafka, DNS server, SQLite, or Git from scratch.

Sign up, and become a better software engineer.

---

What is the two pointers method?

Two-pointers are a highly effective technique that can be applied to a wide range of use cases. If you worked on algorithm problems, you surely came across it, even if you didn't know what it was called this way.

The method uses two integer variables, each representing a position or index in a data structure that can be iterated over, such as an array or a string. The concept is to move these pointers along the data structure in a planned and organized way, using certain properties instead of trying every possible combination at random.

This way, we can turn problems that would need a nested loop with quadratic time complexity into ones that can be solved in linear time. Let's look at the 2Sum problem as an example.

Given a sorted array of size n and a target value, we need to find two numbers that add up to the target. A brute force approach would check every possible pair:

def twoSum_bruteForce(nums, target):
    for i in range(len(nums)):
        for j in range(i+1, len(nums)):
            if nums[i] + nums[j] == target:
                return [i, j]
    return [-1, -1]  # No solution found

This takes O(n²) time because we use nested loops to check all pairs. However, with two pointers, we can solve it in O(n) time:

def twoSum_twoPointers(nums, target):
    left = 0
    right = len(nums) - 1
    
    while left < right:
        current_sum = nums[left] + nums[right]
        
        if current_sum == target:
            return [left, right]
        elif current_sum < target:
            left += 1  # Need a larger sum, so increase left pointer
        else:
            right -= 1  # Need a smaller sum, so decrease right pointer
            
    return [-1, -1]  # No solution found

Why does this work? Since the array is sorted, we know that moving the left pointer to the right increases the sum, and moving the right pointer to the left decreases the sum. So, at each step, we can make an informed decision about the pointer to move, rather than checking all combinations.

While the method may seem easy at first glance, there are several ways to implement it. How we initialize the pointers, move them, and what conditions we check can be very different based on the problem. We'll look at these in more detail below.

Core strategies and templates

The two-pointer technique can be used in different flavors depending on the type of problem we're trying to solve.

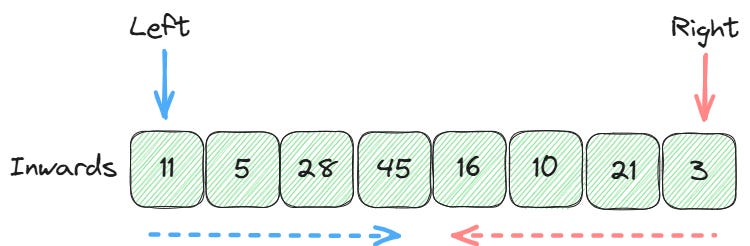
A common strategy is the inward traversal. Here, we put one pointer at the beginning of the data structure and another at its end. Both pointers then move toward each other until they cross or meet.

def inwardTraversal(arr):
    left = 0
    right = arr.length - 1
    
    while left < right:
        // Do something with arr[left] and arr[right]
        // Then move pointers based on some condition
        left++
        right--

This is a great way to solve problems with sorted arrays or palindrome strings. Since the pointers start n positions apart and move closer with each step, you only need O(n) iterations.

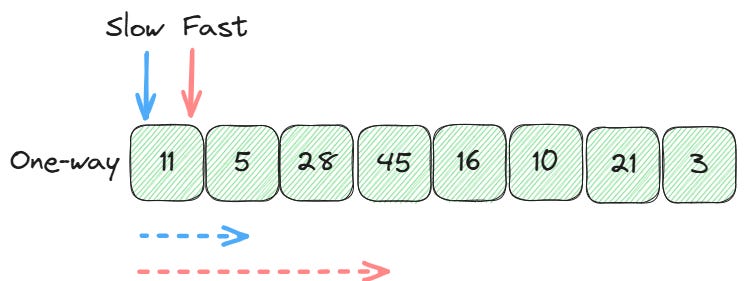
With one-way traversal, both pointers start at the same end and move in the same direction. However, the pointers typically move at different speeds or under different conditions.

def oneWayTraversal(arr):
    slow = 0
    fast = 0
    
    while fast < arr.length:
        // Do something with arr[slow] and arr[fast]
        // Move pointers based on specific conditions
        slow++
        fast += 2  // Or some other rule

This method works well for problems where we need to keep track of two positions at the same time, like moving items to the end of an array or removing duplicates in place.

In the multi-pass traversal, one pointer does the initial work, and then a second pointer takes over when certain conditions are met.