Mastering Linked Lists: A Complete Guide

From traversal to reversal: essential linked list algorithms and techniques to solve common interview problems.

Hi Friends,

Welcome to the 131st issue of the Polymathic Engineer newsletter.

This week, we talk about Linked Lists. The main focus will be on what you need to know to ace coding interview questions, but we will also cover a range of concepts that any developer should understand.

The outline is as follows:

• What is a Linked List?

• Types of Linked Lists

• Implementing a Linked List

• Linked Lists vs. Arrays

• Fast and Slow Pointers Technique

• Reversing a Linked List

---

Project-based learning is the best way to develop technical skills. CodeCrafters is an excellent platform for practicing exciting projects, such as building your version of Redis, Kafka, DNS server, SQLite, or Git from scratch.

Sign up, and become a better software engineer.

---

What is a linked list?

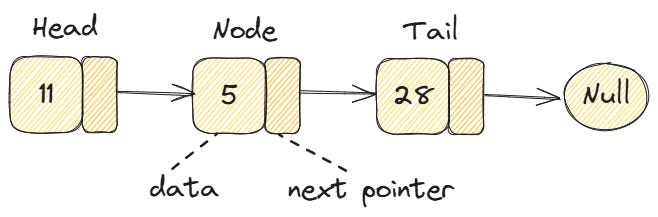
A linked list is a linear data structure that stores elements in a sequence, but unlike an array, these elements are not placed in consecutive memory locations. Instead, each element has the data itself and a "pointer" to the next element in the sequence.

The building blocks of linked lists are called nodes. In its basic form, a node is an object that holds two important pieces of data:

1. Data (or value): the information you want to store

2. Next pointer: A pointer or reference to the next node

Here's what a simple node looks like in Python:

class ListNode:

    def __init__(self, val):

        self.val = val

        self.next = None

When you connect multiple nodes together, you get a linked list. For example, you can represent the sequence [1, 2, 3] by creating three nodes and linking them together:

node1 = ListNode(1)

node2 = ListNode(2)

node3 = ListNode(3)

node1.next = node2

node2.next = node3

# node3.next remains None (end of list)

Two other basic concepts you come across frequently are the head and tail of a linked list:

• Head: The first node in the linked list. This is the entry point to access the entire list.

• Tail: The last node in the linked list. Its next pointer is None, indicating the end of the list.

The head is particularly important because it's the only node you need to keep track of to access the entire linked list. From the head, you can traverse through each node using the next pointers until you reach the tail.

In the next section, we'll explore how linked lists compare to arrays and when you might choose one over the other.

I see this section mentions operations like access, insertion, and search. So I would move it after "Implementing a linked list". Write the section about "types of linked lists" first

Types of Linked Lists

While the general idea is the same – nodes connected through pointers – there are different types of linked list. Each one is made to solve a different problem or offer different features.

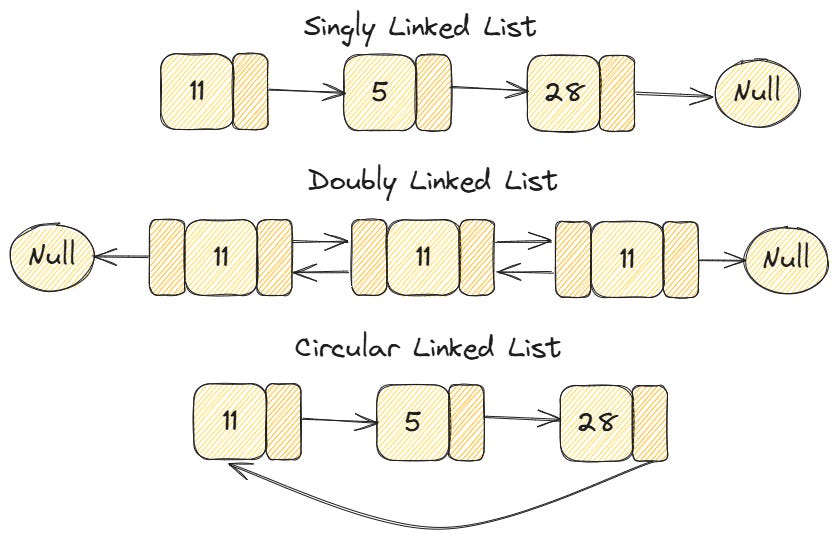
The most basic and common type is the singly linked list, which it is what we've been discussing so far. Here, each node contains data and a single pointer that points to the next node in the sequence. The memory overhead is minimal but you can only traverse in forward direction.

A doubly linked list extends the singly linked list by adding a second pointer to each node. Now, each node points to both the next and the previous node in the sequence. The previous node of the head, and the next node of the tail are `None`.

class DoublyListNode:

    def __init__(self, val):

        self.val = val

        self.next = None

        self.prev = None

The extra pointer in this structure takes up more memory, but you can move through it both in the forward and backward direction. A simple use case where this works well is to build abstract data types, such as deques (double-ended queues), where you can add and remove items from both ends. A helpful concept for doing this efficiently is that of sentinel nodes.

The idea is that, even when there are no nodes in a linked list, you still keep pointers to the head and tail. The actual head of the linked list is head.next, and the actual tail is tail.prev. The sentinel nodes themselves are not part of the linked list. The use of sentinel nodes not only makes it possible to add and remove elements from the front or back of the linked list in O(1) time, but also makes the code doing those operations cleaner, as it is not necessary to have special handling of edge cases, such as an empty list.

In a circular linked list, the last node doesn't point to `None`. Instead, it points back to the first node, creating a circle. Circular lists can be implemented with either singly or doubly linked structures.

Since you can start traversal from any node, there is no true "head" or "tail", node but you need careful handling to avoid infinite loops during traversal.

Even if in most coding interviews and algorithm problems, you only encounter singly linked lists, understanding the variations we discussed in this section will make you a more versatile programmer and help you choose the right tool for each job.

Implementing a Linked List

Now that we understand the different types of linked lists, let's dive into how to build a singly linked list from scratch. We'll use an object oriented approach implementing a basic node structure and then build the essential operations around it:

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None

Traversal is the most basic operation, since it lets you visit each node in the list. This pattern appears in almost every linked list problem and can be implemented using a loop or recursively. The time complexity is O(n) in both cases. The space complexity is O(1) for the iterative version, and O(n) for the recursive because of the call stack.

def traverse(self):
    current = self.head
    while current:
        print(current.val)
        current = current.next

def traverse_recursive(self, node):
    if not node:
        return
    print(node.val)
    self.traverse_recursive(node.next)

Let’s now see how to insert a new node. There are three scenarios to cover: insert at the beginning, at the end, or at a specific position. The first two are straightforward, in the third one the idea is to find the predecessor of the node to be inserted.

def insert_at_beginning(self, val):
    new_node = ListNode(val)
    new_node.next = self.head
    self.head = new_node

def insert_at_end(self, val):
    new_node = ListNode(val)
    if not self.head:
        self.head = new_node
        return
    
    current = self.head
    while current.next:
        current = current.next
    current.next = new_node

def insert_at_position(self, val, position):
    if position == 0:
        self.insert_at_beginning(val)
        return
    
    new_node = ListNode(val)
    current = self.head
    
    for i in range(position - 1):
        if not current:
            return  # Position out of bounds
        current = current.next
    
    if current:
        new_node.next = current.next
        current.next = new_node

Deleting a node is an operation similar to insertion and can happen at the beginning, end, or a specific position. However, the most common thing in algorithmic problems is to delete a node with a specific value.

def delete_value(self, val):
    if not self.head:
        return
    
    if self.head.val == val:
        self.head = self.head.next
        return
    
    current = self.head
    while current.next:
        if current.next.val == val:
            current.next = current.next.next
            return
        current = current.next

The previous code works, but it is complex because it handles the case of empty list explicitly. In all such cases using a dummy node that always keep track of the head can simplify your code.

def delete_value(self, val):
    dummy = ListNode(0)
    dummy.next = self.head
    current = dummy
    
    while current.next:
        if current.next.val == val:
            current.next = current.next.next
        else:
            current = current.next
    
    return dummy.next

The time complexity for inserting and deleting an element with a given value is O(n). However, if you have a reference to the preceding node in the sequence, the operation becomes O(1).

Linked Lists vs. Arrays