Heap Use Cases Every Algorist Should Know
Three must to know applications of the heap data structures: largest elements, graphs, and Huffmann encoding.
Hi Friends,
Welcome to the 146th issue of the Polymathic Engineer newsletter.
When talking about the most fundamental data structures in computer science, heaps don't always get the credit they deserve. Most of the attention is on arrays, linked lists, and hash tables. However, heaps are used by some of the most critical algorithms we use every day.
This week, we will look at three heap use cases that every software engineer who is serious about algorithms and data structures should know. The outline will be as follows:
Heaps
Priority Queues
Finding the K Largest Elements
Graph Algorithms
Huffman Coding
Project-based learning is the best way to develop solid technical skills. CodeCrafters is an excellent platform for tackling exciting projects, such as building your own Git, Redis, Kafka, a DNS server, SQLite, or an HTTP server from scratch.
Sign up, and become a better software engineer.
Heaps
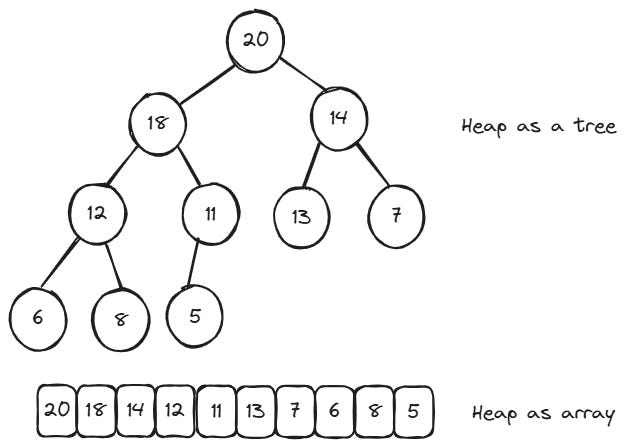
A heap is a type of tree-based data structure with a simple but useful property: in a max-heap, every parent node is greater than or equal to its children, while in a min-heap, every parent is smaller than or equal to its children. This simple constraint makes a data structure that is great at one thing: handling prioritized data speedily.
When you use a GPS to find the shortest route, when you compress files, or when you look at streaming data, there is probably a heap working behind the scenes.
The beauty of heaps lies in their versatility. The same structure can be used to solve a wide range of problems, from traversing graphs to compressing data, and it often works much faster than other methods. If you know when and how to use heaps, you can turn ugly, inefficient algorithms into elegant, scalable ones.
Priority Queues
At its heart, a heap is the most natural implementation of a priority queue, an abstract data type where elements are processed based on their priority rather than on their arrival order. It’s like the emergency room of a triage system: patients aren't seen in the order they arrive, but according to the urgency of their condition.
Priority queues do two basic things: add an item with a certain priority and take out the item with the highest (or lowest) priority. You could use other data structures, like arrays or linked lists, to do these things, but heaps are by far the most efficient way.
If you used an array-based method, it would take O(n) time to either insert elements in the right order or look for the most important element to extract it. Heaps elegantly solve this problem by maintaining their structural property, which takes only O(log n) time.
The key insight is that heaps don't maintain a completely sorted order, but just make sure that the most important element is always at the top. This loose ordering requirement is what makes heaps so efficient. You can insert and extract elements quickly without having to keep the structure fully sorted.
Picking the right kind of heap is very important. With a max-heap, the biggest item is at the top, while with a min-heap, the top item is the smallest. We will see in the next sections that using the wrong type of heap can make a solution less efficient, even if the underlying theory appears to be correct.
Finding the K Largest Elements
One of the most common tasks where heaps really shine is when you need to find the k largest elements from a collection. This problem may seem straightforward, but it's actually quite tricky and highlights why choosing the right data structure and using it correctly matters so much.
Let's say you have a massive dataset with millions of elements, and you only need the top 100. This is a typical scenario in many real-world applications: you might need to find the most shared posts on social media, the students with the best grades, or select the best recommendations from a large pool of options.
If you have all the data upfront, there are a couple of obvious approaches that might come to mind, but they are not great:
Sorting everything: You could sort the entire dataset and pick out the last k items. This requires O(n log n) comparisons and might need extra memory depending on the sorting algorithm. It works, but you're putting in a lot more work than is needed.
Selection sort approach: You could start by moving the largest element to the end of the list. Then you could look through the rest of the list to find the next largest element, and so on. This basically means to run the inner loop of selection sort k times. It needs O(k) swaps and O(n*k) comparisons, with no extra memory. Better than sorting everything when k is small, but still not optimal.
Using a heap structure, we can solve the problem with O(n + k*log k) comparisons and swaps, and O(k) extra memory. This is a huge improvement if k is much smaller than n, which is usually the case in practice. The key insight is that we don't need a huge data structure to track everything. We just need a small heap that keeps track of the k largest elements we've seen so far.
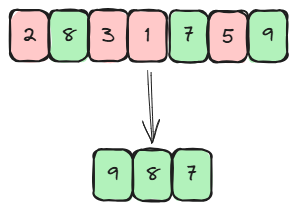
However, there is a point at which many people become confused. You might think that a max-heap would be the best way to find the largest item, right? But that would be the wrong answer. Let's see why with a simple example. Suppose we want to select the three largest numbers from the following list: 11, 14, 11, 13, 17, 16.
If we use a max-heap and add the first three numbers, we get [14, 12, 11]. Now, when we get the next number (13), we know it's larger than some elements in our heap, but we can only see the largest element. If we insert 13, we'd need to remove the smallest one so that we only have three left. However, finding the minimum element in a max-heap might take linear time, as it is hidden among the leaves.
The solution is counterintuitive but brilliant: use a min-heap of size k. In this way, the smallest of our k largest elements will always be at the top of the heap. When we get a new number, we compare it to the top. If it's smaller, we don't mind. If it's bigger, we take off the top and add the new number.
import heapq
def top_k(A, k):
"""Find the k largest elements using a min-heap"""
heap = []
for el in A:
if len(heap) == k and heap[0] < el:
heapq.heappop(heap) # Remove the smallest element
if len(heap) < k:
heapq.heappush(heap, el) # Insert the element
return heap