Fundamental Graph Algorithms Part III: DFS On Directed Graphs

How depth-first search shines on directed graphs: topological sorting and strongly connected component algorithms

Dec 13, 2025

∙ Paid

Hi Friends,

Welcome to the 152nd issue of the Polymathic Engineer newsletter.

This week, we will complete our in-depth series of articles about fundamental graph algorithms and their applications. In particular, we will discuss the most critical uses of depth-first search on undirected graphs. The outline will be the following:

What is Topological Sorting
How to use DFS for Topological Sorting
Implementation
Strongly Connected Components
The Two-Pass Algorithm
Implementation
A concrete example

Project-based learning is the best way to develop technical skills. CodeCrafters is an excellent platform for tackling exciting projects, such as building your own Redis, Kafka, a DNS server, SQLite, or Git from scratch.

What is Topological Sorting

Topological sorting is an algorithm that puts the vertices of a directed acyclic graph (DAG) in a linear order such that for every directed edge (u, v), vertex u appears before vertex v in the ordering. If you visualize vertices along a horizontal line, all directed edges point from left to right.

Looking at this definition, it’s clear that this order can only work if there are no loops in the graph. Indeed, it's not possible to keep going straight on a line and end up back where you started if there is a loop.

This sorting operation is critical for scheduling problems. Consider building software in which some modules depend on others, compiling code in which some files need to be processed before others, or taking university courses with prerequisites. In all such cases, you need an ordering that respects the dependencies. That is what a topological sort gives you.

Still, this is just the tip of the iceberg since topological sorting is a preprocessing step for almost all algorithms operating on DAGs. For example, to find the longest path in a DAG, you can process vertices in topological order. Since you deal with each vertex after all its predecessors, you can compute the longest path to each vertex one step at a time without worrying about missing any incoming edges.

How to use DFS for Topological Sorting

The most important thing to understand is that DFS automatically generates a reverse topological ordering based on its finishing times. Once you have explored all outgoing edges from a vertex, you can safely add it to the reversed topological order. The reason is that you have already handled everything the vertex depends on.

Let's consider what may happen to each directed edge (u, v) during a DFS run. There are three possibilities:

If v is undiscovered, we start a DFS from v before continuing with u. This means v finishes before u, so u appears before v in the reverse order, which is exactly what we want.
If v is already discovered but not yet processed, (u, v) is a back edge, which means the graph has a cycle. This contradicts our assumption that the graph is a DAG.
If v is already processed, it has been processed before u. Therefore, v will be added to the topological order before u, and when we reverse the order, u will come before v, as desired.

Once you understand these three points, the algorithm is simple: perform a DFS on the graph and push each vertex onto a stack when you finish processing it. Popping out the vertices from the stack gives you the topological order.

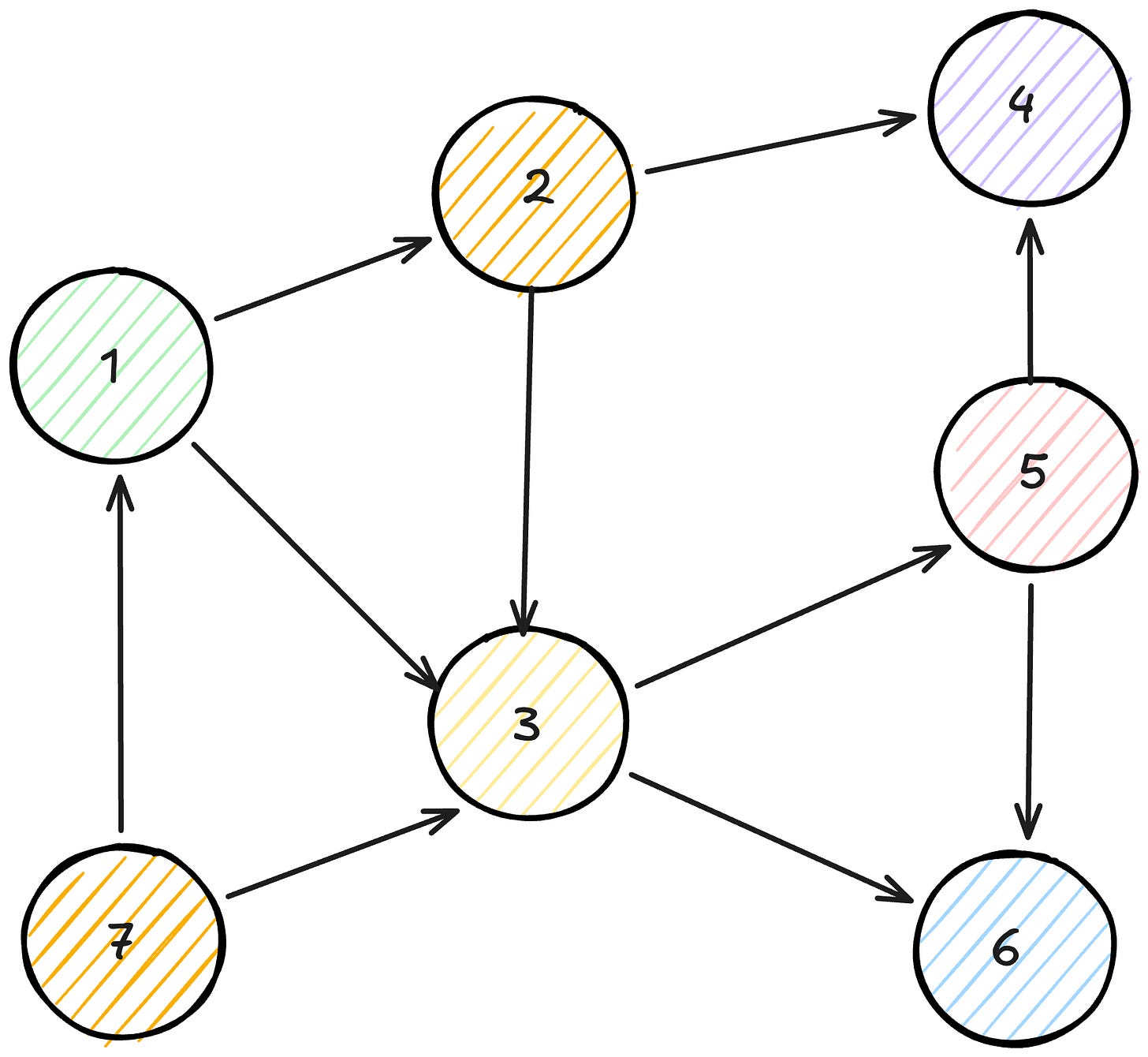
Let’s walk through an example using a graph with vertices (1→2), (1→3), (2→3), (2→4),(3→5), (3→6), (5→4), (6→5), (7→6), (7→1). This could represent a build system where each vertex is a module and edges represent dependencies (module u must be built before module v).

Starting DFS from vertex 1, this is what happens:

Discover vertex 1, explore its first neighbor 2
Discover vertex 2, explore its first neighbor 3
Discover vertex 3, explore its first neighbor 5
Discover vertex 5, explore its first neighbor 4
Discover vertex 4, no outgoing edges (vertex 4 is marked processed and added to the stack)
Backtrack to vertex 5 (vertex 5 is marked processed and added to the stack)
Backtrack to vertex 3, explore its second neighbor 6
Discover vertex 6, which has no more undiscovered neighbors (vertex 6 is marked processed and added to the stack)
Backtrack to vertex 3 (vertex 3 is marked processed and added to the stack)
Backtrack to vertex 2, which has no more undiscovered neighbors (vertex 2 is marked processed and added to the stack)
Backtrack to vertex 1, which has no more undiscovered neighbors (vertex 1 is marked processed and added to the stack)
Check for undiscovered vertices, find vertex 7
Discover vertex 7, which has no more undiscovered neighbors (vertex 7 is marked processed and added to the stack)

The vertices finish in this order: 4, 5, 6, 3, 2, 1, 7, and the final topological order is: 7, 1, 2, 3, 6, 5, 4. You can verify that this ordering is valid by checking that each edge points from left to right.

Implementation

Here is a possible implementation of the topological sorting using DFS:

class TopologicalSort(DFS):
    def __init__(self, graph):
        super().__init__(graph)
        self.sorted_vertices = []
        self.has_cycle = False
    
    def postprocess_vertex(self, vertex):
        # Add vertex to the beginning of the list (equivalent to pushing to stack)
        self.sorted_vertices.insert(0, vertex)
    
    def process_edge(self, from_vertex, to_vertex):
        edge_type = self.edge_classification(from_vertex, to_vertex)
        
        if edge_type == “BACK”:
            self.has_cycle = True
            print(f”Warning: cycle detected at edge ({from_vertex}, {to_vertex})”)
            print(”Graph is not a DAG - topological sort not possible”)
            self.finished = True
    
    def topological_sort(self):
        “”“Perform topological sort on the graph”“”
        self.search_all()
        
        if self.has_cycle:
            return None
        
        return self.sorted_vertices

The implementation uses insert(0, vertex) to add vertices to the front of a list, which is equivalent to pushing them onto a stack and then reversing. Alternatively, you could append to the list and reverse it at the end, or use an actual stack and pop elements. The time complexity is O(V + E), dominated by the DFS traversal. Building the topological order adds only a constant amount of work per vertex.

Finally, an important thing to keep in mind is that a DAG can have multiple correct topological orders, all of which respect the dependencies. You get a different sorting depending on the order in which you look at neighbors in DFS.

Strongly Connected Components

A strongly connected component (SCC) is a maximal set of vertices in a directed graph where there is a path between every pair of vertices. In other words, you can reach any vertex from any other vertex within the same component by following directed edges.

The Polymathic Engineer