Data Structures for Image Processing
Five data structures you should know to write great image processing algorithms.
Hi Friends,
Welcome to the 114th issue of the Polymathic Engineer newsletter.
To be a better software engineer, you must know much about the most popular data structures. But if you work in a very narrow domain, this might not be enough on its own. One example of this is image processing.
This week, we talk about specialized data structures that are important for writing image processing algorithms that are efficient and work well.
The outline will be as follows:
Matrices
Chains
Graphs
Pyramids
Quadtrees
Project-based learning is the best way to develop technical skills. CodeCrafters is an excellent platform for practicing exciting projects, such as building your version of Redis, Kafka, DNS server, SQLite, or Git from scratch.
Sign up, and become a better software engineer.
Matrices
Matrices are the most basic and widely used data structures in image processing. They are the backbone for low-level representation of images, providing an effective way to store and manipulate pixel data.
A matrix typically has integer elements, each corresponding to a pixel's brightness or another property in the image grid. Such information is easily accessible through row and column indices corresponding to pixel coordinates.
Matrices implicitly contain spatial relationships between different parts of the image, making working with neighborhoods and adjacencies easy.
A downside is that matrices can be memory-intensive. However, modern computers usually have sufficient RAM to handle them, even for large images.
While matrices are excellent for low-level image representation, they can be expensive for complex operations. This is why more advanced data structures are used with or as alternatives to simple matrices.
Chains
Chains are data structures commonly used to describe object borders in an image.
The idea is to represent data as a sequence of symbols, where neighboring symbols usually correspond to neighboring pixels in the image.
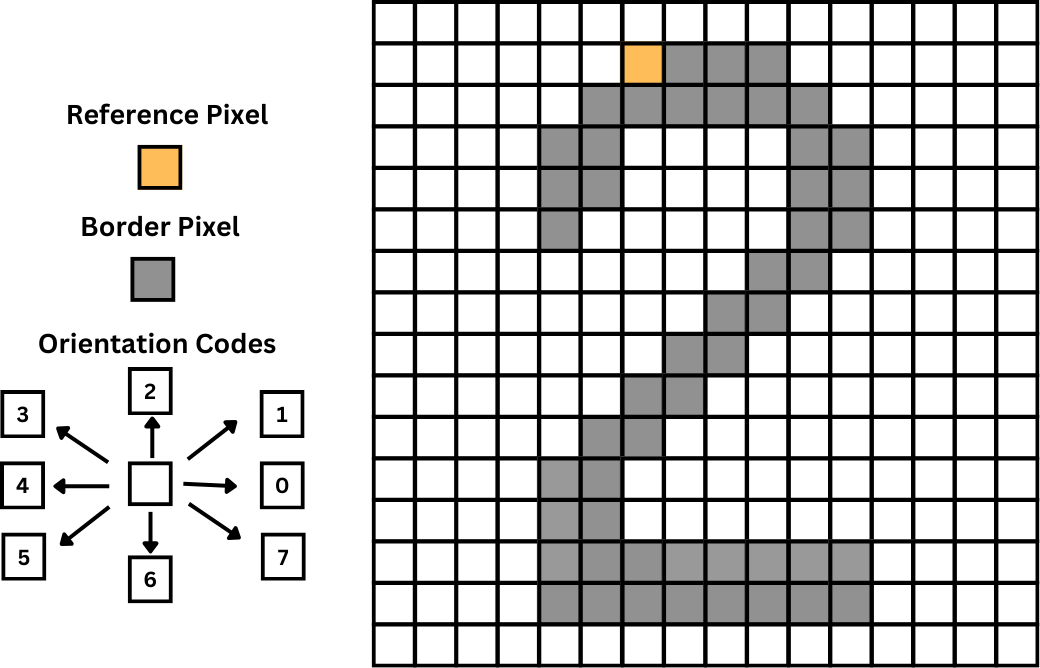
The most popular application of chains is chain codes, which are used to represent one-pixel-wide lines. A chain code defines a border by referencing a specific pixel's coordinates and providing a sequence of symbols that correspond to one-pixel-length lines in predefined orientations.
In the picture below, if we consider the orange pixel as a reference, the corresponding chain code would be:
00077665555556600000006444444442221111112234445652211
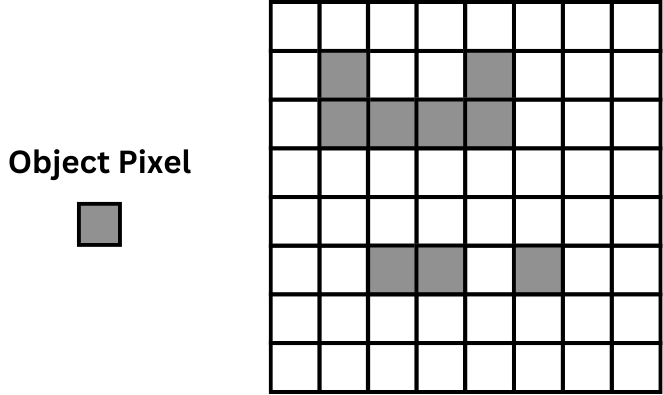
An alternative application of chains is run-length coding, which is used to represent objects. Given an image matrix as an input, run-length coding records only the areas that belong to the object in the image.
Typically, each row of the image is represented by a list. The first element of the list is the row number, while the other elements are pairs of column coordinates. The first element of a pair is the beginning of a pixel sequence, and the second is the end.
In the picture below, the corresponding run length coding would be: [[11144], [214], [52355]].
An advantage of chains is that they can be represented using basic data structures like arrays or lists and can be easily used for pattern recognition.
However, chains have limitations. First, they are linear data structures that cannot directly describe complex spatial relationships in an image. Second, accessing pixel-related information from a chain requires sequentially searching through the entire structure.
Graphs
Topological data structures like graphs are powerful tools for describing images in terms of elements and their relationships.
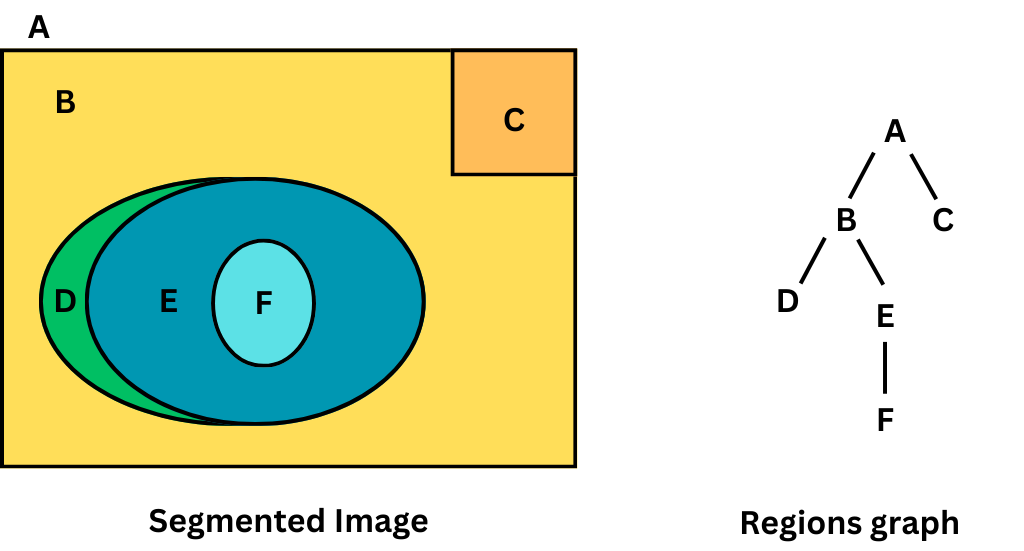
A graph consists of a set of nodes and a set of arcs connecting these nodes. In image processing, nodes often represent regions or objects that have been segmented in the image, while arcs represent relationships between these regions.
Region adjacency graphs are a common application of graphs in image processing. In such kinds of graphs:
Each node represents a distinct region in the segmented image.
Arcs connect nodes representing adjacent regions.
The graph structure explicitly stores neighborhood information.
Region adjacency graphs have several useful properties:
They efficiently represent spatial relationships between regions.
Graph cuts can identify enclosed regions.
Nodes with a degree of 1 represent simple holes.
Additional information (like 'left of' or 'inside') can be stored in the arcs.
To create a region adjacency graph, you typically start with an image matrix where each element is an identifier for the region it belongs to. You can then construct the graph by tracing region borders and recording adjacent region labels.
Pyramids
Pyramids are hierarchical data structures that can represent an image at multiple resolutions. They are handy for algorithms that need to work with different levels of detail simultaneously.
There are two main types of pyramids: Matrix-pyramids (M-pyramids) and Tree-pyramids (T-pyramids).
An M-pyramid is a sequence of images where each level is derived from the previous one by reducing the resolution by half. The original picture is at the pyramid's base, and a single pixel is at the top. This data structure makes it easy to get to versions of in versions of images with lower resolution, which can significantly speed up specific processing tasks.
For example, in the picture below, the red box indicates the size of a template used for detecting flying birds. Since the template size is fixed, it can only detect the birds that tightly fit inside the box. Different birds are detected at different scales by running the same template across many levels in this pyramid.
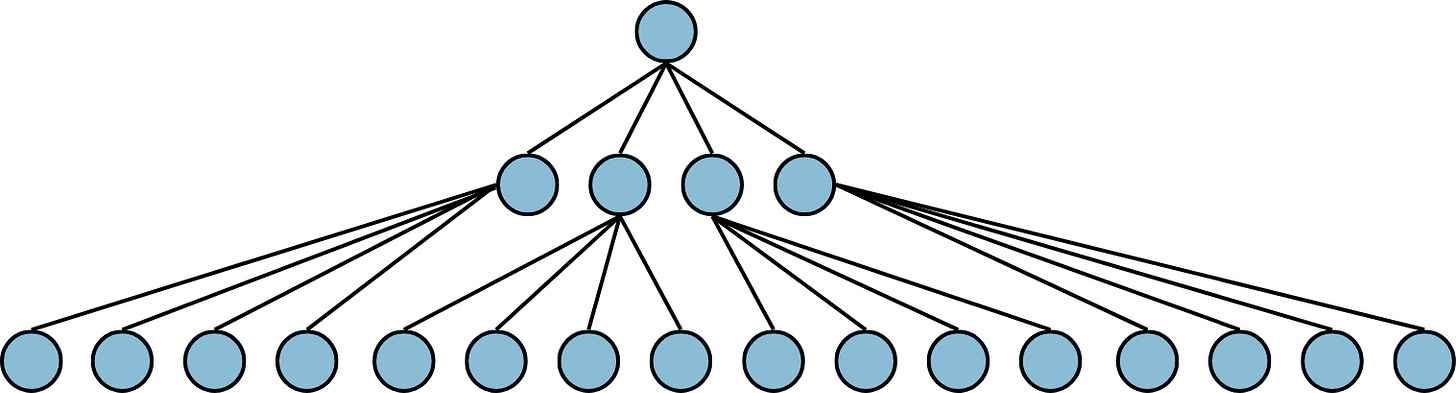
T-pyramids, on the other hand, organize the multi-resolution data in a tree structure.
Each node in the tree corresponds to a pixel at a specific resolution level, with leaf nodes representing pixels in the original image. The value of each non-leaf node is typically derived from its child nodes, often by averaging their values.
The key advantage of pyramids is their ability to support algorithms that adapt their processing based on image content. For example, an algorithm might work at coarse resolutions in areas with little detail and switch to finer resolutions only in complex regions of the image.
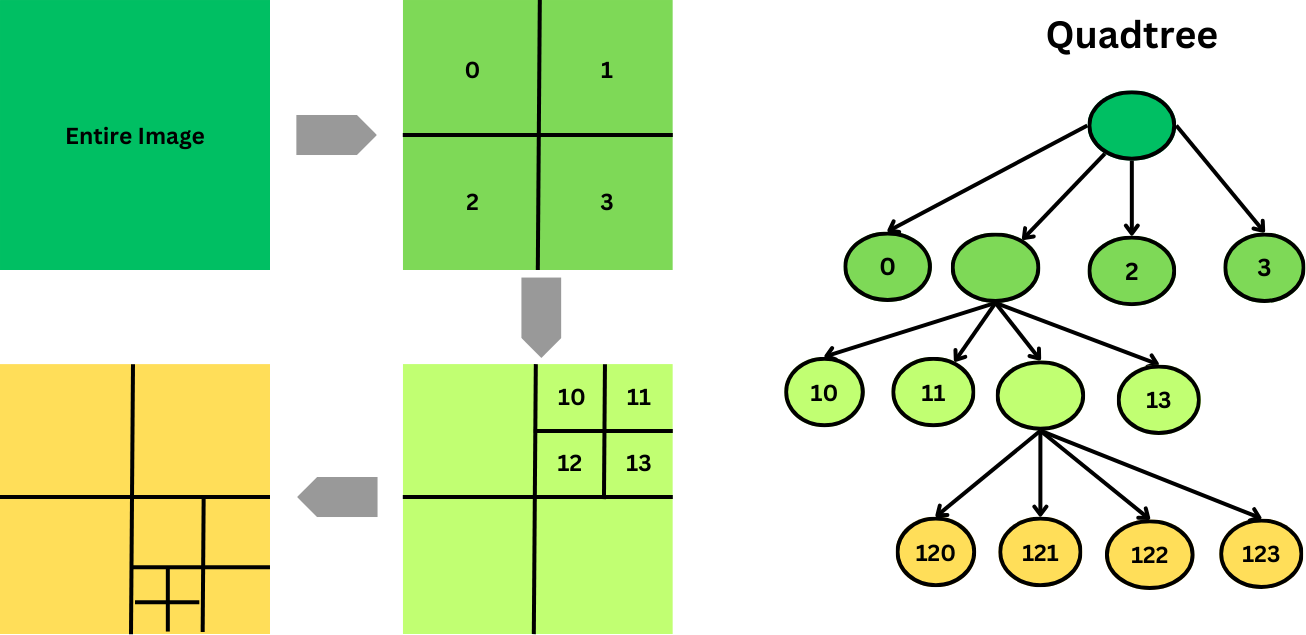
Quadtrees
Quadtrees are hierarchical data structures that provide an efficient way to represent images with large homogeneous regions. They modify T-pyramids, where each non-leaf node has exactly four children.
The basic idea is to divide an image into four quadrants recursively. If all pixels in a quadrant have the same value, that quadrant is represented by a single node. If not, the quadrant is further divided into four sub-quadrants. This process continues until all pixels in a sub-quadrant are homogeneous or a single pixel is reached.
The main advantage of quadtrees is that their representation is much more compact than storing every pixel individually, especially for images with large, uniform areas. Moreover, simple algorithms exist for computing object areas or adding images.
The main disadvantage is that quadtrees heavily depend on the position, orientation, and relative size of objects. Two similar images with just very small differences can have very different quadtree representations.
Interesting Reading
Some interesting articles I read recently:



Love it.